In copertina foto di Markus Spiske da Pexels

A sinistra (A) c’è un grafico, palesemente errato, condiviso su Twitter il 29 Aprile 2020.
A destra (B) c’è un grafico costruito sugli stessi dati, utilizzando il modo corretto di operare.
Analizziamo i due grafici e scopriamo perché sono diversi.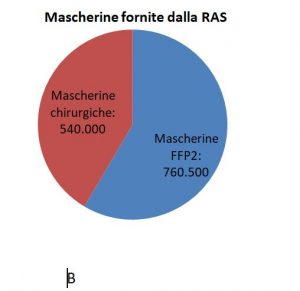
Entrambi sono grafici a torta, così chiamati perché ciascuna modalità viene raffigurata sotto forma di una fetta di torta, che è proporzionale al valore che rappresenta.
Nel grafico A, la torta è formata da 3 spicchi, quello più grande identifica il totale delle mascherine fornite dalla RAS (1.300.500), mentre, i due più piccoli, i dati relativi alla distribuzione di mascherine chirurgiche (540.000) e di tipo FFP2(760.500), rispettivamente. Basta eseguire un semplice calcolo matematico, un’addizione per l’esattezza, per renderci conto che il grafico è privo di senso, infatti 540.000 + 760.500 = 1.300.500, quindi lo spicchio che rappresenta il totale non ha ragione di esistere: le mascherine sono state distribuite tutte.
Nel grafico B, la torta è formata da 2 spicchi relativi, rispettivamente, alle due tipologie di mascherine fornite.
La rappresentazione di una serie di dati, attraverso l’utilizzo di un grafico a torta, rende la comprensione dei risultati più facile e più immediata, grazie anche alla possibilità di giocare con i colori per identificare le serie rappresentate. Inoltre consente di “relativizzare” i risultati, cioè di valutare il rapporto di ciascuna fetta rispetto all’ intera torta. E’ per questo motivo che i risultati vengono molto spesso espressi come percentuali.
Guardiamo il grafico B: la percentuale di mascherine chirurgiche rispetto al totale è pari al [(540.000 : 1.300.500) x 100] = 41,5%, mentre quella delle FFP2, al [(760.500 : 1.300.500) x 100] = 58,5%.
Quali altre caratteristiche deve avere un grafico a torta per essere considerato attendibile e comprensibile?
Se abbiamo una variabile costituita da molte modalità da rappresentare, è meglio optare per un grafico diverso: a barre (se si tratta di un fenomeno discreto) o ad istogrammi (se si tratta di un fenomeno continuo). Affinché il grafico a torta sia leggibile al primo colpo d’occhio, deve essere formato da poche modalità, al massimo 5.

È importante anche verificare se il grafico a torta rispecchia in modo fedele la matrice dei dati: se quindi le frequenze sono state correttamente trasformate in gradi di una circonferenza. I principali software per la Statistica o anche Excel (usato per costruire il grafico B) eseguono i calcoli in modo automatico.
Ma se non si avessero a disposizione strumenti di questo tipo? Come si procede?
Ritorniamo al grafico B: il totale delle mascherine corrisponde alla nostra torta, che non è altro che un cerchio.
Dividiamo il totale per 360°, che è il valore dell’ampiezza dell’angolo al centro del cerchio, pari ad un angolo giro: 1.300.500 : 360° = 3.612,5 che corrisponde al numero di mascherine che coprono un angolo di ampiezza pari ad 1°.
Poiché a ciascuna tipologia di mascherine raffigurate nel disegno dovrebbe corrispondere uno spicchio di torta, calcoliamo l’ampiezza esatta dell’angolo da occupare, dividendo ciascun tipo per il valore dell’angolo di ampiezza 1°; per le mascherine chirurgiche avremo: 540.000 : 3.612,5 = 149,5°; per le mascherine FFp2: 760.500 : 3.612,5 = 210,5°
A questo punto, servendosi di un goniometro, si possono riportare sul cerchio i valori delle ampiezze degli angoli trovati, al fine di assegnare a ciascuna frequenza lo spicchio giusto.
Cosa abbiamo imparato?
In Statistica non si può improvvisare, anche se si ricorre all’ausilio di software o di Excel una minima conoscenza di ciò che si va a fare è sempre richiesta per non incorrere in errori.
Cosa considerare in una lettura attenta di un grafico?
Valutare sempre con occhio attento ciò che si sta guardando e non lasciarsi trarre in inganno da grafici belli a vedersi, ma non in grado di rappresentare fedelmente la realtà.
Diffidare da grafici che non mostrano i dati di partenza, verificare la corrispondenza delle scale, delle unità di misura e delle grandezze indicate sugli assi ortogonali X e Y.
Nel caso di grafici a linee accertarsi che sia specificato il punto zero (il punto di inizio del grafico), soprattutto se non coincide con l’origine degli assi cartesiani.
Se si sta guardando un istogramma chiedersi se i dati rappresentati fanno parte di una distribuzione continua, per esempio la rappresentazione di gruppi di individui per classi d’età, altrimenti le conclusioni che ne derivano sono falsate, a causa della scelta sbagliata del tipo di grafico. In caso di dati discreti, infatti, occorre usare il diagramma a barre, una sorta di istogramma con i rettangoli separati invece che affiancati.
La correttezza nell’esecuzione di un grafico è molto importante, perché altrimenti si rischia di dare una rappresentazione alterata di un fenomeno. È recente la confusione scatenata dai grafici sul numero di morti per Covid-19: i dati non distinguevano tra i deceduti per altre cause e quelli per l’infezione da coronavirus, e l’informazione che ne scaturiva era un alto indice di mortalità. Questo errore ha richiesto una normalizzazione dei dati ed una smentita successiva da parte delle autorità.


Comments